Numba Example

(Back to Overview)

JIT-compiled (thread) parallel python code: https://gist.github.com/safijari/fa4eba922cea19b3bc6a693fe2a97af7

We want to solve a silly version of the (under) damped spring-mass problem

def friction_fn(v, vt):
    if v > vt:
        return - v * 3
    else:
        return - vt * 3 * np.sign(v)


def simulate_spring_mass_funky_damper(x0, T=10, dt=0.0001, vt=1.0):
    times = np.arange(0, T, dt)
    positions = np.zeros_like(times)

    v = 0
    a = 0
    x = x0
    positions[0] = x0/x0

    for ii in range(len(times)):
        if ii == 0:
            continue
        t = times[ii]
        a = friction_fn(v, vt) - 100*x
        v = v + a*dt
        x = x + v*dt
        positions[ii] = x/x0

    return times, positions

plot(*simulate_spring_mass_funky_damper(0.1))
plot(*simulate_spring_mass_funky_damper(1))
plot(*simulate_spring_mass_funky_damper(10))
legend(['0.1', '1', '10'])

savefig("ts_python.png")
close()

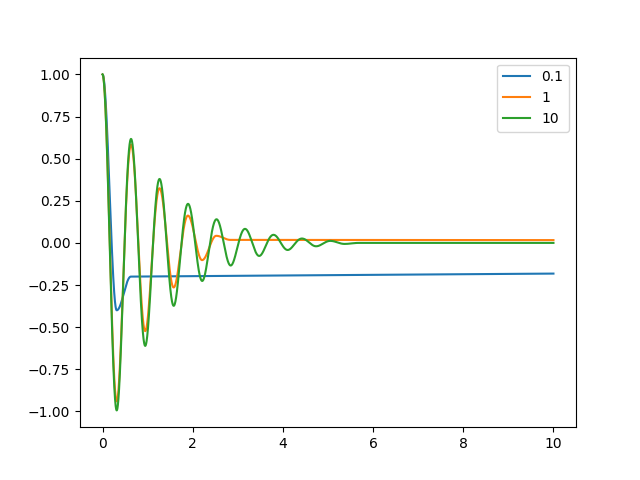
This code generates a time series of the (normalized) position given its different initial position:

%time _ = simulate_spring_mass_funky_damper(1)

CPU times: user 232 ms, sys: 4.7 ms, total: 237 ms
Wall time: 236 ms

Compile with Numba

Remember to use the njit decorator, to disable (slow) python support

from numba import njit

@njit
def numba_friction_fn(v, vt):
    if v > vt:
        return - v * 3
    else:
        return - vt * 3 * np.sign(v)

@njit
def numba_simulate_spring_mass_funky_damper(x0, T=10, dt=0.0001, vt=1.0):
    times = np.arange(0, T, dt)
    positions = np.zeros_like(times)
    
    v = 0
    a = 0
    x = x0
    positions[0] = x0/x0
    
    for ii in range(len(times)):
        if ii == 0:
            continue
        t = times[ii]
        a = numba_friction_fn(v, vt) - 100*x
        v = v + a*dt
        x = x + v*dt
        positions[ii] = x/x0
    return times, positions

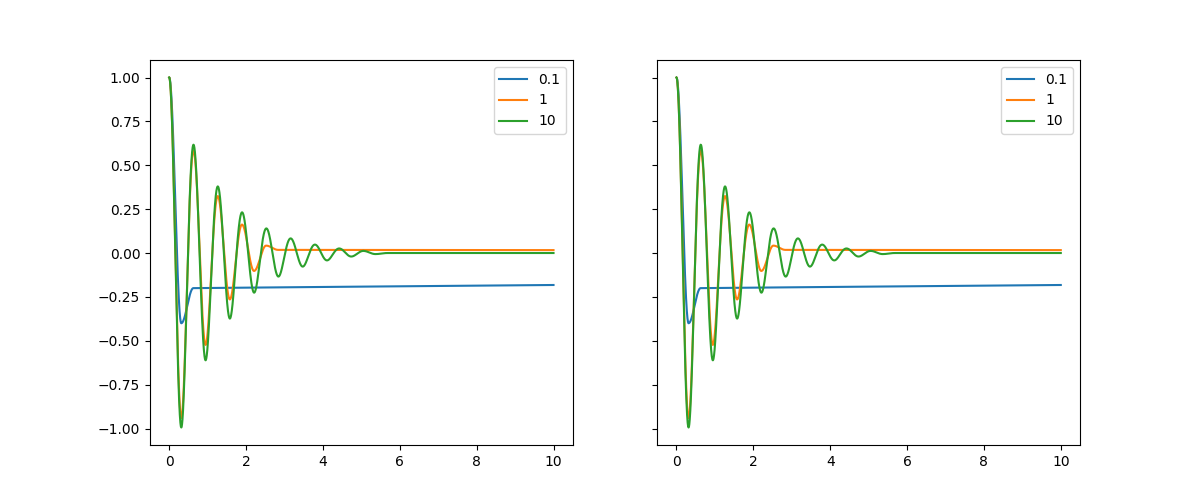
Numba-generated a time series (left) vs original python version (right):

%time _ = simulate_spring_mass_funky_damper(1)

CPU times: user 213 ms, sys: 2.8 ms, total: 216 ms
Wall time: 215 ms

%time _ = numba_simulate_spring_mass_funky_damper(1)

CPU times: user 1.33 ms, sys: 45 µs, total: 1.37 ms
Wall time: 1.4 ms